Electrostatics due to its long-range nature is a key factor in characterizing biomolecular interactions. The methodology to determine electrostatic potential around molecules is often based on the Poisson-Boltzmann mesoscopic theory describing the electrostatic potential and equilibrium distribution of ions around molecules in solution. In this model a molecule is represented as a set of partial charges immersed in implicit solvent with ions modeled by Boltzmann distribution. The resulting Poisson-Boltzmann equation is solved numerically on a three dimensional grid to obtain the electrostatic potential in each grid point.
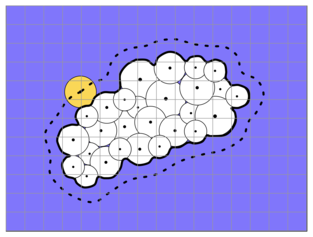
Figure: Schematic representation of the molecule and solvent in the Poisson-Boltzmann model. White spheres denote molecule’s atoms described with point partial charges and van derWaals radii. Biomolecular interior is assigned a dielectric constant between 4 and 20 and the surrounding solvent – 80. The boundary between the solute and the solvent is shown as dotted line.
- Beyond the Poisson-Boltzmann Model – Finite Size of Ions
Because RNA is a highly charged molecule, description of its electrostatics requires improved methodology and proper treatment of counter ions. In the standard Poisson-Boltzmann model ionic strength is represented by a Boltzmann distribution which neglects the finite size of ions. We have developed a simple modification of this model to account for the finite size of ions by applying a cutoff in the concentration formula for ionic distribution at regions of high electrostatic potentials [1]. The effect of this cutoff is significant up to 4-5°A from the molecular surface.
- Electrostatic Similarity by Spherical Harmonic Decomposition of Electrostatic Potential Grids
We have been developing methods to efficiently compare various properties of biomolecules in order to cluster structurally diverse sets of molecules according to their electrostatic and hydrophobic features. Recently, we developed a method to compare the electrostatics of molecules without their prior structural alignment. It is based on spherical harmonic decomposition of the electrostatic potential grids derived from the Poisson-Boltzmann model [2]. Our method is implemented within Surface Diver, a tool for describing properties on molecular surfaces, available for download in the Software section.
[1] M. Gruziel, P. Grochowski, J. Trylska, J. Comp. Chem., 29:1970, 2008
[2] M. Dlugosz, J. Trylska, J. Chem. Phys., 129:015103, 2008
